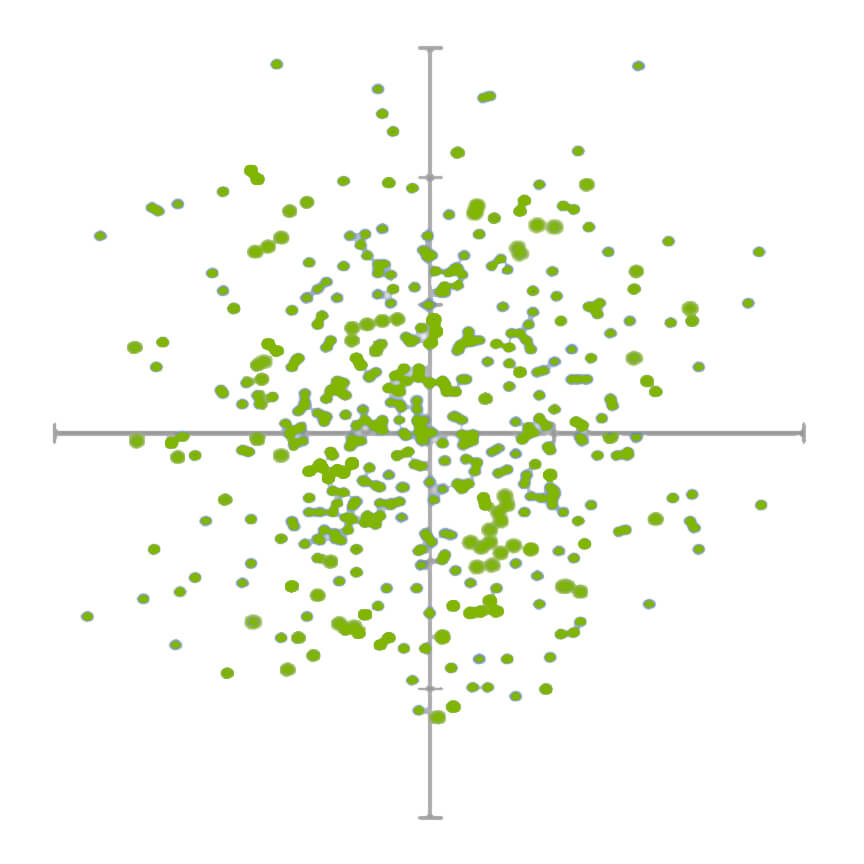
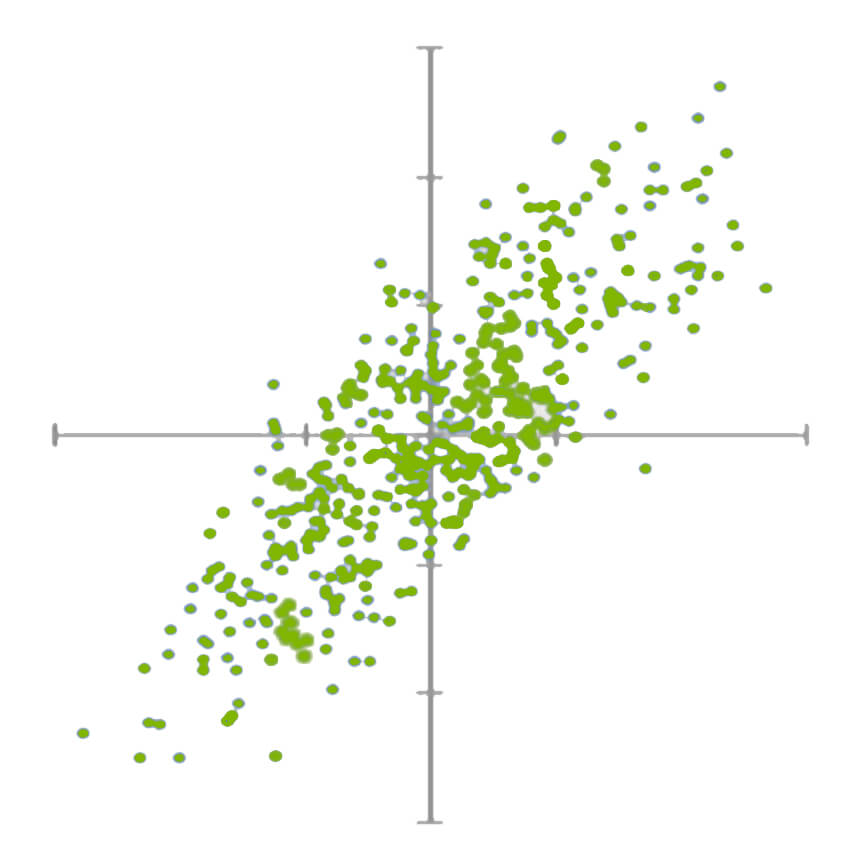
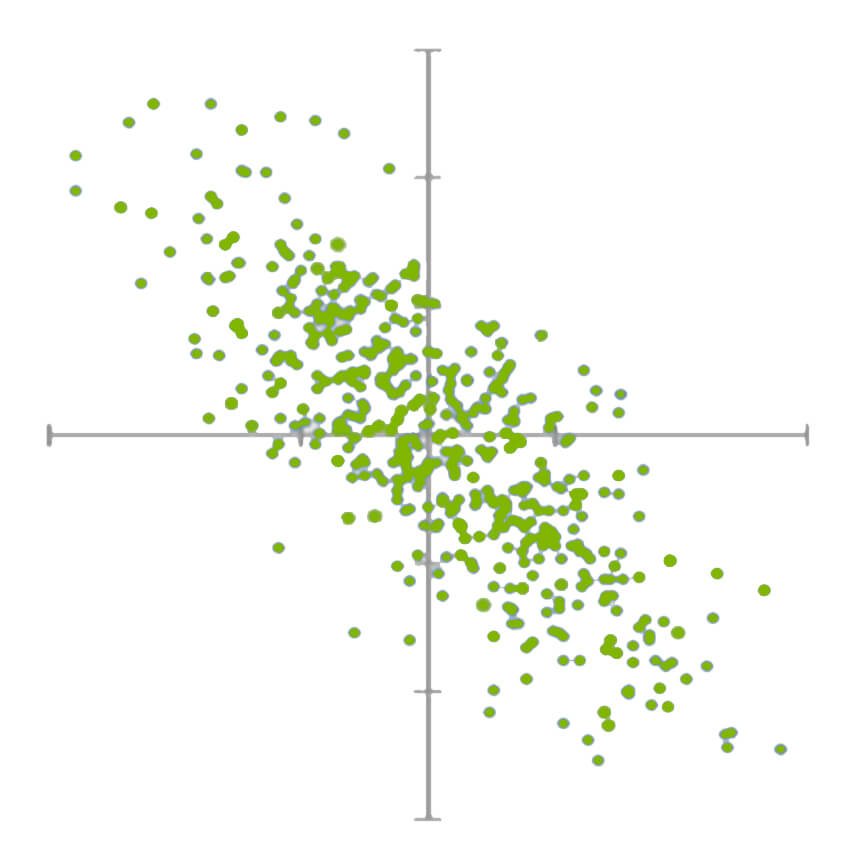
Correlation measures how closely two random variables shift together. It scales the two variables' covariance between -1 and 1 by multiplying the two variables' standard deviations and then dividing the covariance by the result.
The correlation coefficient implies how positively or negatively correlated the two variables are, with numbers between 0 and 1 being positively correlated and -1 and 0 being negatively correlated. Coefficients of 1 and -1 imply a perfect positive or negative correlation.
$$Positive\; Correlation\;$$
$$Negative\; Correlation\;$$
$$No\; Correlation\;$$